
176
Глава 4.
где £0 и ju0 соответственно диэлектрическая и магнитная проницаемости вакуума.
Таким образом, налицо противоречие теории с реальностью. Обращает на себя внимание неполнота вывода третьего уравнения Максвелла (рис. 6.17).
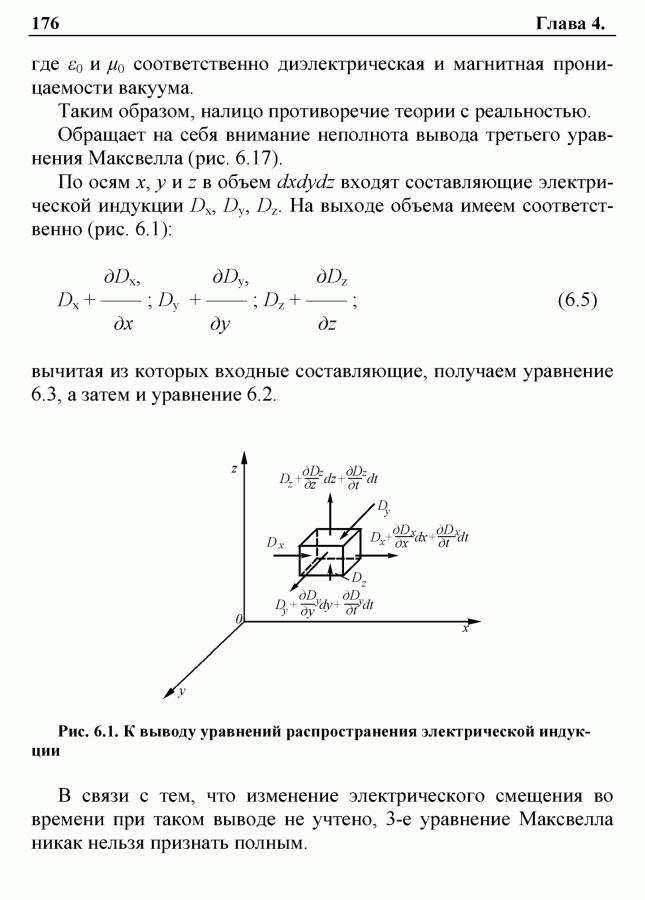
По осям х, у и z в объем dxdydz входят составляющие электрической индукции Dx, Dy, Dz. На выходе объема имеем соответственно (рис. 6.1):
dDx, dDy, dDz
Dx +-; Dy +-; Dz +-; (6.5)
dx dy dz
вычитая из которых входные составляющие, получаем уравнение 6.3, а затем и уравнение 6.2.
Рис. 6.1. К выводу уравнений распространения электрической индукции
В связи с тем, что изменение электрического смещения во времени при таком выводе не учтено, 3-е уравнение Максвелла никак нельзя признать полным.
Эксперименты в области электромагнитных явлений
177
На самом деле, на выходе объема составляющие вектора индукции будут равны:
dDx, dDx, dDy, dDy dDz dDz
Dx +--+--; Dy +--+-; Dz +--+--; (6.6)
dx dt dy dt dz dt
и соответственно 3-е уравнение Максвелла приобретет вид: dD
divD +--= 0. (6.7)
c dt
где скорость с распространения волнового фронта связана с проекциями по осям координат выражением:
1 1 1 1 +--+-. (6.8)
2 2 2 с сх су с
Полученное уравнение есть волновое уравнение первой степени, которое показывает, что электрическая индукция D распространяется в направлении вектора D, т.е. в продольном, а не поперечном направлении. Деление вектора D на вектор скорости с говорит о том, что эти вектора коллинеарны, т.е. параллельны друг другу. Решением уравнения 6.7. будет волновая функция:
D(r - ct) = 0. (6.9)
Отсюда вытекает, что диполь с сосредоточенными параметрами будет излучать энергию во все стороны (рис. 6.2), причем, если расстояние между пульсирующими зарядами (электродами) будет равно половине длины волны, то энергия вдоль оси диполя