
387
сквозь левую грань
– Dydxdz; (8.200)
сквозь правую грань
дDy дDy
(Dy + —— dy + —— dt) dxdz; (8.201)
дy дt
сквозь нижнюю грань
– Dzdxdy; (8.202)
сквозь верхнюю грань
дDz дDz
(Dz + —— dz + —— dt) dxdy; (8.203)
дz дt
Суммируя потоки через все грани и деля их сумму на объем параллелепипеда, находим:
дD
дDy дDz дDz
дх
cx дt дy cy дt
дz
czдt
(8.204)
где
сx = dx/dt; сy= dy/dt; сz= dz/dt; и таким образом,
(8.205)
дD
дDy дD
div D + —— + —— + —— = ρ, cx дt cy дt czдt
(8.206)
1
1
1
1
cx
cy
cz
(8.207)
дDx дDx
2
c
388
или
дD div D + —— = ρ, (8.208)
c дt
что отличается от третьего уравнения Максвелла наличием члена дD/cдt.
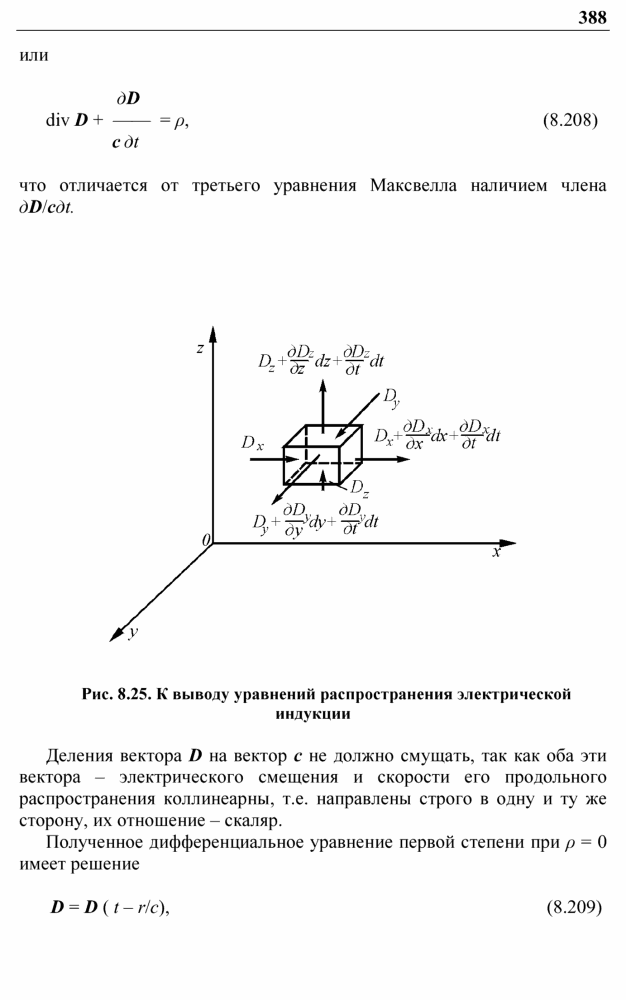
Рис. 8.25. К выводу уравнений распространения электрической индукции
Деления вектора D на вектор с не должно смущать, так как оба эти вектора – электрического смещения и скорости его продольного распространения коллинеарны, т.е. направлены строго в одну и ту же сторону, их отношение – скаляр.
Полученное дифференциальное уравнение первой степени при ρ = 0 имеет решение
D = D ( t – r/c),
(8.209)