
380
двумя уравнениями. Если бы это учитывалось, то как электрическая, так и магнитная напряженности не всегда были бы одними и теми же для первого и второго уравнений.
Наконец, все уравнения Максвелла выведены из предположения об идеальности эфира и, следовательно, подразумевают отсутствие у него вязкости и сжимаемости. В таком эфире вихри не могут ни образовываться, ни исчезать, что полностью не соответствует опытным данным: напряжения и магнитные поля возникают и исчезают, но это не заложено в физику уравнений. В физику уравнений Максвелла также не заложена сжимаемость полей, непосредственно вытекающая из сжимаемости эфира.
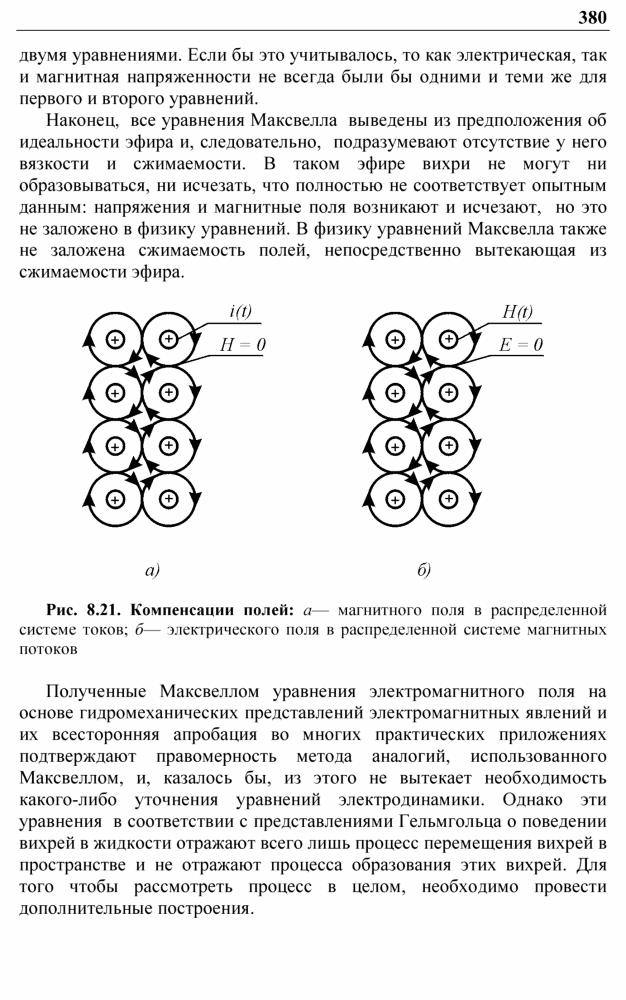
Рис. 8.21. Компенсации полей: а— магнитного поля в распределенной системе токов; б— электрического поля в распределенной системе магнитных потоков
Полученные Максвеллом уравнения электромагнитного поля на основе гидромеханических представлений электромагнитных явлений и их всесторонняя апробация во многих практических приложениях подтверждают правомерность метода аналогий, использованного Максвеллом, и, казалось бы, из этого не вытекает необходимость какого-либо уточнения уравнений электродинамики. Однако эти уравнения в соответствии с представлениями Гельмгольца о поведении вихрей в жидкости отражают всего лишь процесс перемещения вихрей в пространстве и не отражают процесса образования этих вихрей. Для того чтобы рассмотреть процесс в целом, необходимо провести дополнительные построения.
381
Таким образом, уравнения электродинамики Максвелла не являются совершенными, как не является совершенным ничто на свете. И поэтому над ними нужно продолжать работать.
8.4.2. Некоторые уточнения уравнений электродинамики
Рассмотрим элементарный объем среды, находящейся под воздействием приложенной ЭДС, а также внешних магнитных полей (рис. 8.22).
Рис. 8.22. Образование электри- Рис. 8.23. Образование магнитного
ческого тока в среде. потока в среде.
С учетом модели электрического поля вытекает, что ток является следствием электрической напряженности, действующей в цепи, а магнитное поле вокруг проводника является следствием упорядоченной ориентации в проводнике электрических зарядов. Для элемента среды в данной цепи необходимо учитывать четыре электрических напряженности, суммирующиеся друг с другом и создающие электрический ток: Еφ – напряженность от внешнего источника ЭДС; ЕН v1 – напряженность, наводимую со стороны других токов, меняющихся во времени, внешних по отношению к рассматриваемому объему; следует помнить, что магнитное поле, создающее эту ЭДС само имеет волновой характер; ЕН v2 – напряженность, наводимую со стороны движущегося относите-льно рассматриваемого объема источника.
Плотность тока δе, возникающего в цепи, определяется этими напряженностями и проводимостью среды. В свою очередь, ток вызовет магнитное поле, напряженность которого равна ЕН L, так что